Depth First Traversal or Depth First Search is a edge based recursive algorithm for traversing (visiting) all the vertices of a graph or tree data structure using a stack. The purpose of the algorithm is to mark each vertex as visited while avoiding cycles. DFS traverse/visit each vertex exactly once and each edge is inspected exactly twice. DFS is a genuinely recursive algorithm that uses stack for backtracking purposes, not for storing the vertex discovery “front” (as is the case in BFS).
The DFS algorithm works as follows:
- Start by putting any one of the graph’s vertices on top of a stack.
- Take the top item of the stack and add it to the visited list.
- Create a list of that vertex’s adjacent nodes. Add the ones which aren’t in the visited list to the top of the stack.
- Keep repeating steps 2 and 3 until the stack is empty.
DFS example step-by-step:
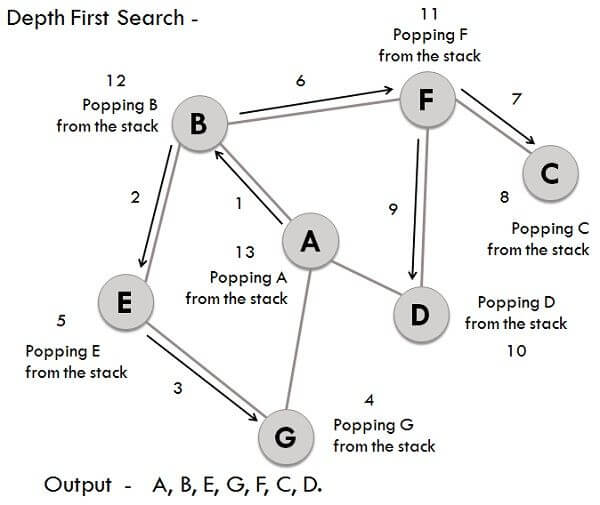
- Considering A as the starting vertex which is explored and stored in the stack.
- B successor vertex of A is stored in the stack.
- Vertex B have two successors E and F, among them alphabetically E is explored first and stored in the stack.
- The successor of vertex E, i.e., G is stored in the stack.
- Vertex G have two connected vertices, and both are already visited, so G is popped out from the stack.
- Similarly, E s also removed.
- Now, vertex B is at the top of the stack, its another node(vertex) F is explored and stored in the stack.
- Vertex F has two successor C and D, between them C is traversed first and stored in the stack.
- Vertex C only have one predecessor which is already visited, so it is removed from the stack.
- Now vertex D connected to F is visited and stored in the stack.
- As vertex D doesn’t have any unvisited nodes, therefore D is removed.
- Similarly, F, B and A are also popped.
- The generated output is – A, B, E, G, F, C, D.