Morris (In-Order) traversal is a tree traversal algorithm that does not employ the use of recursion or a stack. In this traversal, links are created as successors and nodes are printed using these links. Finally, the changes are reverted back to restore the original tree.
Basically a tree is threaded by making all right child pointers that would normally be null point to the inorder successor of the node (if it exists), and all left child pointers that would normally be null point to the inorder predecessor of the node. Consider:
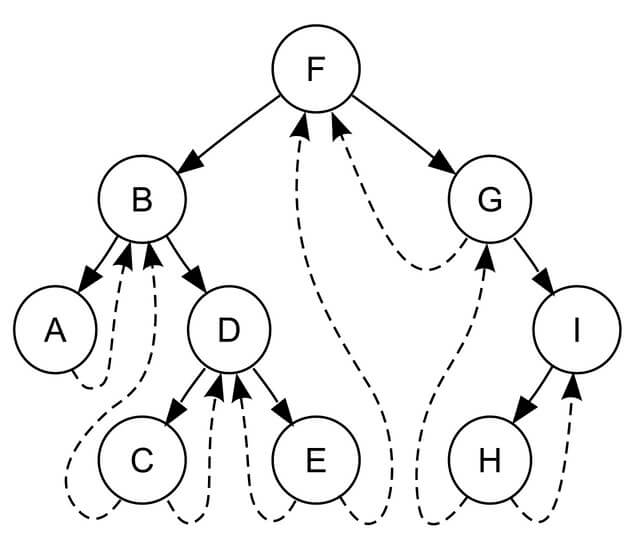
Algorithm:
- Initialize the
rootas the current nodecurr. - While
curris notNULL, check ifcurrhas a left child. - If
currdoes not have a left child, printcurrand update it to point to the node on the right ofcurr. - Else, make
currthe right child of the rightmost node incurr‘s left subtree. - Update
currto this left node.
Complexity Analysis
The way of looking at time complexity is to find out how many times a tree node will be traversed. As it is constant (3 times for a binary tree). So we are looking at O(n).
Implementation
public class MorrisPreorderTraversal { static class Node { //static class to represent node structure int data; //to store data of each node Node left, right; //to point to left and right child of the node respectively Node(int d) { //constructor for initialisation of each values this.data = d; this.left = null; this.right = null; } } public static void printPreorder(Node root) { if (root == null) { //if tree is empty return; } while (root != null) { if (root.left == null) { //if left child is empty System.out.print(root.data + " "); //traverse current node and root = root.right; //move to it's right } else { Node curr = root.left; //to store inorder predecessor while (curr.right != null && curr.right != root) { curr = curr.right; } if (curr.right == root) { //if right child of inorder predecessor points to root node itself curr.right = null; root = root.right; } else { //otherwise System.out.print(root.data + " "); //traverse current node curr.right = root; //make right child of inorder predecessor point to this node root = root.left; } } } } public static void main(String args[]) { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.left = new Node(6); root.right.right = new Node(7); printPreorder(root); }}/* -:Sample Input Tree:- 1 / \ 2 3 / \ / \ 4 5 6 7-:Sample Output:-1 2 4 5 3 6 7 -:Time Complexity:-O(n) where n is the number of nodes in the given tree-:Space Complexity:-O(1) */

