Lowest Common Ancestor

Table of Contents

1. Lowest Common Ancestor – $O(\sqrt{N})$ and $O(\log N)$ with $O(N)$ preprocessing
2. The Idea of the Algorithm
3. Implementation
4. Practice Problems

1. Lowest Common Ancestor – $O(\sqrt{N})$ and $O(\log N)$ with $O(N)$ preprocessing

Given a tree $G$ . Given queries of the form $(v_1, v_2)$ , for each query you need to find the lowest common ancestor (or least common ancestor), i.e. a vertex $v$ that lies on the path from the root to $v_1$ and the path from the root to $v_2$ , and the vertex should be the lowest. In other words, the desired vertex $v$ is the most bottom ancestor of $v_1$ and $v_2$ . It is obvious that their lowest common ancestor lies on a shortest path from $v_1$ and $v_2$ . Also, if $v_1$ is the ancestor of $v_2$ , $v_1$ is their lowest common ancestor.

2. The Idea of the Algorithm

Before answering the queries, we need to preprocess the tree. We make a DFS traversal starting at the root and we build a list $\text{euler}$ which stores the order of the vertices that we visit (a vertex is added to the list when we first visit it, and after the return of the DFS traversals to its children). This is also called an Euler tour of the tree. It is clear that the size of this list will be $O(N)$ . We also need to build an array $\text{first}[0..N-1]$ which stores for each vertex $i$ its first occurrence in $\text{euler}$ . That is, the first position in $\text{euler}$ such that $\text{euler}[\text{first}[i]] = i$ . Also by using the DFS we can find the height of each node (distance from root to it) and store it in the array $\text{height}[0..N-1]$ .

So how can we answer queries using the Euler tour and the additional two arrays? Suppose the query is a pair of $v_1$ and $v_2$ . Consider the vertices that we visit in the Euler tour between the first visit of $v_1$ and the first visit of $v_2$ . It is easy to see, that the $\text{LCA}(v_1, v_2)$ is the vertex with the lowest height on this path. We already noticed, that the LCA has to be part of the shortest path between $v_1$ and $v_2$ . Clearly it also has to be the vertex with the smallest height. And in the Euler tour we essentially use the shortest path, except that we additionally visit all subtrees that we find on the path. But all vertices in these subtrees are lower in the tree than the LCA and therefore have a larger height. So the $\text{LCA}(v_1, v_2)$ can be uniquely determined by finding the vertex with the smallest height in the Euler tour between $\text{first}(v_1)$ and $\text{first}(v_2)$ .

Let’s illustrate this idea. Consider the following graph and the Euler tour with the corresponding heights:

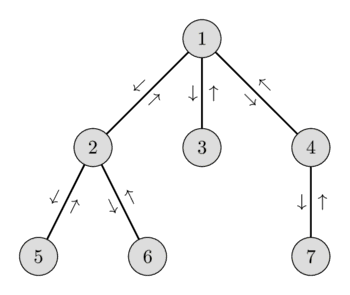
$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{Vertices:} & 1 & 2 & 5 & 2 & 6 & 2 & 1 & 3 & 1 & 4 & 7 & 4 & 1 \\ \hline \text{Heights:} & 1 & 2 & 3 & 2 & 3 & 2 & 1 & 2 & 1 & 2 & 3 & 2 & 1 \\ \hline \end{array}$

The tour starting at vertex $6$ and ending at $4$ we visit the vertices $[6, 2, 1, 3, 1, 4]$ . Among those vertices the vertex $1$ has the lowest height, therefore $\text{LCA(6, 4) = 1}$ .

To recap: to answer a query we just need to find the vertex with smallest height in the array $\text{euler}$ in the range from $\text{first}[v_1]$ to $\text{first}[v_2]$ . Thus, the LCA problem is reduced to the RMQ problem (finding the minimum in an range problem).

Using Sqrt-Decomposition, it is possible to obtain a solution answering each query in $O(\sqrt{N})$ with preprocessing in $O(N)$ time.

Using a Segment Tree you can answer each query in $O(\log N)$ with preprocessing in $O(N)$ time.

Since there will almost never be any update to the stored values, a Sparse Table might be a better choice, allowing $O(1)$ query answering with $O(N\log N)$ build time.

3. Implementation

In the following implementation of the LCA algorithm a Segment Tree is used.

struct LCA {
    vector<int> height, euler, first, segtree;
    vector<bool> visited;
    int n;
 
    LCA(vector<vector<int>> &adj, int root = 0) {
        n = adj.size();
        height.resize(n);
        first.resize(n);
        euler.reserve(n * 2);
        visited.assign(n, false);
        dfs(adj, root);
        int m = euler.size();
        segtree.resize(m * 4);
        build(1, 0, m - 1);
    }
 
    void dfs(vector<vector<int>> &adj, int node, int h = 0) {
        visited[node] = true;
        height[node] = h;
        first[node] = euler.size();
        euler.push_back(node);
        for (auto to : adj[node]) {
            if (!visited[to]) {
                dfs(adj, to, h + 1);
                euler.push_back(node);
            }
        }
    }
 
    void build(int node, int b, int e) {
        if (b == e) {
            segtree[node] = euler[b];
        } else {
            int mid = (b + e) / 2;
            build(node << 1, b, mid);
            build(node << 1 | 1, mid + 1, e);
            int l = segtree[node << 1], r = segtree[node << 1 | 1];
            segtree[node] = (height[l] < height[r]) ? l : r;
        }
    }
 
    int query(int node, int b, int e, int L, int R) {
        if (b > R || e < L)
            return -1;
        if (b >= L && e <= R)
            return segtree[node];
        int mid = (b + e) >> 1;
 
        int left = query(node << 1, b, mid, L, R);
        int right = query(node << 1 | 1, mid + 1, e, L, R);
        if (left == -1) return right;
        if (right == -1) return left;
        return height[left] < height[right] ? left : right;
    }
 
    int lca(int u, int v) {
        int left = first[u], right = first[v];
        if (left > right)
            swap(left, right);
        return query(1, 0, euler.size() - 1, left, right);
    }
};