Limak is a little polar bear. He doesn’t have many toys and thus he often plays with polynomials.
He considers a polynomial valid if its degree is n and its coefficients are integers not exceeding k by the absolute value. More formally:
Let a 0, a 1, …, a n denote the coefficients, so 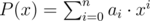 . Then, a polynomial P(x) is valid if all the following conditions are satisfied:
. Then, a polynomial P(x) is valid if all the following conditions are satisfied:
- a i is integer for every i;
- |a i| ≤ k for every i;
- a n ≠ 0.
Limak has recently got a valid polynomial P with coefficients a 0, a 1, a 2, …, a n. He noticed that P(2) ≠ 0 and he wants to change it. He is going to change one coefficient to get a valid polynomial Q of degree n that Q(2) = 0. Count the number of ways to do so. You should count two ways as a distinct if coefficients of target polynoms differ.
Input
The first line contains two integers n and k (1 ≤ n ≤ 200 000, 1 ≤ k ≤ 109) — the degree of the polynomial and the limit for absolute values of coefficients.
The second line contains n + 1 integers a 0, a 1, …, a n (|a i| ≤ k, a n ≠ 0) — describing a valid polynomial 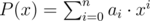 . It’s guaranteed that P(2) ≠ 0.
. It’s guaranteed that P(2) ≠ 0.
Output
Print the number of ways to change one coefficient to get a valid polynomial Q that Q(2) = 0.
Examples
input
3 1000000000
10 -9 -3 5
output
3
input
3 12
10 -9 -3 5
output
2
input
2 20
14 -7 19
output
0
Note
In the first sample, we are given a polynomial P(x) = 10 - 9x - 3x 2 + 5x 3.
Limak can change one coefficient in three ways:
- He can set a 0 = - 10. Then he would get Q(x) = - 10 - 9x - 3x 2 + 5x 3 and indeed Q(2) = - 10 - 18 - 12 + 40 = 0.
- Or he can set a 2 = - 8. Then Q(x) = 10 - 9x - 8x 2 + 5x 3 and indeed Q(2) = 10 - 18 - 32 + 40 = 0.
- Or he can set a 1 = - 19. Then Q(x) = 10 - 19x - 3x 2 + 5x 3 and indeed Q(2) = 10 - 38 - 12 + 40 = 0.
In the second sample, we are given the same polynomial. This time though, k is equal to 12 instead of 109. Two first of ways listed above are still valid but in the third way we would get |a 1| > k what is not allowed. Thus, the answer is 2 this time.
Solution:
#include <bits/stdc++.h>
using namespace std;
const long long inf = (long long) 1e18;
const int N = 1234567;
long long a[N], b[N];
int main() {
int n, k;
scanf("%d %d", &n, &k);
n++;
for (int i = 0; i < n; i++) {
int foo;
scanf("%d", &foo);
a[i] = foo;
}
long long z = 0;
int up = 0;
for (int i = 0; i < n; i++) {
z += a[i];
b[i] = z;
if (z % 2 != 0) {
break;
}
up++;
z /= 2;
}
long long value = 0;
int ans = 0;
for (int i = n - 1; i >= 0; i--) {
if (i <= up) {
long long tmp = value * 2 + b[i];
long long z = a[i] - tmp;
if (-k <= z && z <= k && (i != n - 1 || z != 0)) {
ans++;
}
}
value = value * 2 + a[i];
if (value < -inf || value > inf) {
break;
}
}
printf("%d\n", ans);
return 0;
}

