User ainta has a permutation p 1, p 2, …, p n. As the New Year is coming, he wants to make his permutation as pretty as possible.
Permutation a 1, a 2, …, a n is prettier than permutation b 1, b 2, …, b n, if and only if there exists an integer k (1 ≤ k ≤ n) where a 1 = b 1, a 2 = b 2, …, a k - 1 = b k - 1 and a k < b k all holds.
As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of p i and p j (1 ≤ i, j ≤ n, i ≠ j) if and only if A i, j = 1.
Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.
Input
The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.
The second line contains n space-separated integers p 1, p 2, …, p n — the permutation p that user ainta has. Each integer between 1 and n occurs exactly once in the given permutation.
Next n lines describe the matrix A. The i-th line contains n characters ‘0’ or ‘1’ and describes the i-th row of A. The j-th character of the i-th line A i, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, A i, j = A j, i holds. Also, for all integers i where 1 ≤ i ≤ n, A i, i = 0 holds.
Output
In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.
Examples
input
7
5 2 4 3 6 7 1
0001001
0000000
0000010
1000001
0000000
0010000
1001000
output
1 2 4 3 6 7 5
input
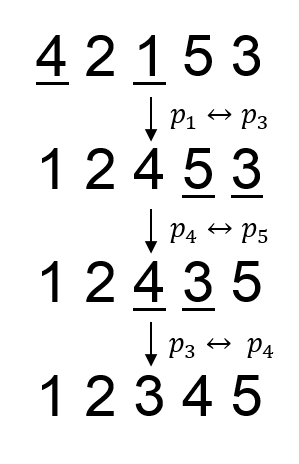
5
4 2 1 5 3
00100
00011
10010
01101
01010
output
1 2 3 4 5
Note
In the first sample, the swap needed to obtain the prettiest permutation is: (p 1, p 7).
In the second sample, the swaps needed to obtain the prettiest permutation is (p 1, p 3), (p 4, p 5), (p 3, p 4).
A permutation p is a sequence of integers p 1, p 2, …, p n, consisting of n distinct positive integers, each of them doesn’t exceed n. The i-th element of the permutation p is denoted as p i. The size of the permutation p is denoted as n.
Solution:
#include <cstring>
#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <stack>
#include <bitset>
#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <sstream>
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <memory.h>
#include <cassert>
using namespace std;
const int N = 777;
char s[N][N];
int value[N];
int a[N];
bool was[N];
int x[N];
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", a + i);
}
for (int i = 0; i < n; i++) {
scanf("%s", s[i]);
}
for (int i = 0; i < n; i++) {
was[i] = false;
}
for (int i = 0; i < n; i++) {
if (was[i]) {
continue;
}
int b = 0, e = 0;
x[0] = i;
was[i] = true;
while (b <= e) {
for (int j = 0; j < n; j++) {
if (!was[j] && s[x[b]][j] == '1') {
e++;
x[e] = j;
was[j] = true;
}
}
b++;
}
for (int pos = 0; pos <= e; pos++) {
value[pos] = a[x[pos]];
}
sort(x, x + e + 1);
sort(value, value + e + 1);
for (int pos = 0; pos <= e; pos++) {
a[x[pos]] = value[pos];
}
}
for (int i = 0; i < n - 1; i++) {
printf("%d ", a[i]);
}
printf("%d\n", a[n - 1]);
return 0;
}

