Today Pari and Arya are playing a game called Remainders.
Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value 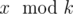 . There are n ancient numbers c 1, c 2, …, c n and Pari has to tell Arya
. There are n ancient numbers c 1, c 2, …, c n and Pari has to tell Arya 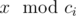 if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value
if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value 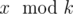 for any positive integer x?
for any positive integer x?
Note, that 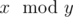 means the remainder of x after dividing it by y.
means the remainder of x after dividing it by y.
Input
The first line of the input contains two integers n and k (1 ≤ n, k ≤ 1 000 000) — the number of ancient integers and value k that is chosen by Pari.
The second line contains n integers c 1, c 2, …, c n (1 ≤ c i ≤ 1 000 000).
Output
Print “Yes” (without quotes) if Arya has a winning strategy independent of value of x, or “No” (without quotes) otherwise.
Examples
input
4 5
2 3 5 12
output
Yes
input
2 7
2 3
output
No
Note
In the first sample, Arya can understand 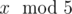 because 5 is one of the ancient numbers.
because 5 is one of the ancient numbers.
In the second sample, Arya can’t be sure what 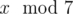 is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.
is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.
Solution:
#include <bits/stdc++.h>
using namespace std;
inline int gcd(int a, int b) {
while (a > 0 && b > 0) {
if (a > b) {
a %= b;
} else {
b %= a;
}
}
return a + b;
}
inline int lcm(int a, int b) {
return a / gcd(a, b) * b;
}
int main() {
int n, k;
scanf("%d %d", &n, &k);
int l = 1;
for (int i = 0; i < n; i++) {
int x;
scanf("%d", &x);
int g = gcd(x, k);
l = lcm(l, g);
}
puts(l == k ? "Yes" : "No");
return 0;
}

