AND Graph - VietMX's Blog

You are given a set of size $m$ with integer elements between $0$ and $2^{n}-1$ inclusive. Let’s build an undirected graph on these integers in the following way: connect two integers $x$ and $y$ with an edge if and only if $x \& y = 0$ . Here $\&$ is the bitwise AND operation. Count the number of connected components in that graph.

Input

In the first line of input there are two integers $n$ and $m$ ( $0 \le n \le 22$ , $1 \le m \le 2^{n}$ ).

In the second line there are $m$ integers $a_1, a_2, \ldots, a_m$ ( $0 \le a_{i} < 2^{n}$ ) — the elements of the set. All $a_{i}$ are distinct.

Output

Print the number of connected components.

Examples

input

2 3
1 2 3

output

input

5 5
5 19 10 20 12

output

Note

Graph from first sample:

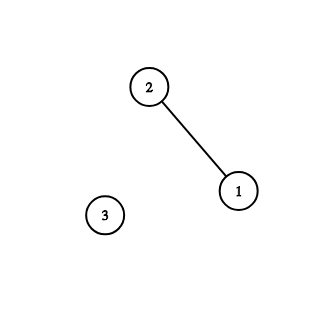
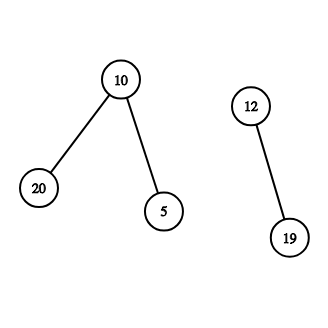
Graph from second sample:

Solution:

#include <bits/stdc++.h>
 
using namespace std;
 
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> n >> m;
vector<int> was(1 << n, 1);
  for (int i = 0; i < m; i++) {
    int x;
    cin >> x;
was[x] = 0;
}
vector<int> used(1 << n, 0);
  vector<int> que(1 << n);
  vector<int> inner(1 << n);
  int ans = 0;
  for (int start = 0; start < (1 << n); start++) {
    if (was[start]) {
      continue;
    }
    ans++;
    was[start] = 1;
    que[0] = start;
    int qs = 1;
    for (int q = 0; q < qs; q++) {
      int u = (1 << n) - 1 - que[q];
      if (!used[u]) {
        used[u] = 1;
        inner[0] = u;
        int is = 1;
        for (int i = 0; i < is; i++) {
          int z = inner[i];
          if (!was[z]) {
            was[z] = 1;
            que[qs++] = z;
          }
          for (int bit = 0; bit < n; bit++) {
            if ((z & (1 << bit)) && !used[z ^ (1 << bit)]) {
              used[z ^ (1 << bit)] = 1;
              inner[is++] = z ^ (1 << bit);
            }
          }
        }
      }
    }
  }
  cout << ans << '\n';
  return 0;
}