Bear and Two Paths

Bearland has n cities, numbered 1 through n. Cities are connected via bidirectional roads. Each road connects two distinct cities. No two roads connect the same pair of cities.

Bear Limak was once in a city a and he wanted to go to a city b. There was no direct connection so he decided to take a long walk, visiting each city exactly once. Formally:

• There is no road between a and b.
• There exists a sequence (path) of n distinct cities v ₁, v ₂, …, v _n that v ₁ = a, v _n = b and there is a road between v _i and v _i + 1 for .

On the other day, the similar thing happened. Limak wanted to travel between a city c and a city d. There is no road between them but there exists a sequence of n distinct cities u ₁, u ₂, …, u _n that u ₁ = c, u _n = d and there is a road between u _i and u _i + 1 for .

Also, Limak thinks that there are at most k roads in Bearland. He wonders whether he remembers everything correctly.

Given n, k and four distinct cities a, b, c, d, can you find possible paths (v ₁, …, v _n) and (u ₁, …, u _n) to satisfy all the given conditions? Find any solution or print -1 if it’s impossible.

Input

The first line of the input contains two integers n and k (4 ≤ n ≤ 1000, n - 1 ≤ k ≤ 2n - 2) — the number of cities and the maximum allowed number of roads, respectively.

The second line contains four distinct integers a, b, c and d (1 ≤ a, b, c, d ≤ n).

Output

Print -1 if it’s impossible to satisfy all the given conditions. Otherwise, print two lines with paths descriptions. The first of these two lines should contain n distinct integers v ₁, v ₂, …, v _n where v ₁ = a and v _n = b. The second line should contain n distinct integers u ₁, u ₂, …, u _n where u ₁ = c and u _n = d.

Two paths generate at most 2n - 2 roads: (v ₁, v ₂), (v ₂, v ₃), …, (v _n - 1, v _n), (u ₁, u ₂), (u ₂, u ₃), …, (u _n - 1, u _n). Your answer will be considered wrong if contains more than k distinct roads or any other condition breaks. Note that (x, y) and (y, x) are the same road.

Examples

input

7 11
2 4 7 3

output

2 7 1 3 6 5 4
7 1 5 4 6 2 3

input

1000 999
10 20 30 40

output

-1

Note

In the first sample test, there should be 7 cities and at most 11 roads. The provided sample solution generates 10 roads, as in the drawing. You can also see a simple path of length n between 2 and 4, and a path between 7 and 3.

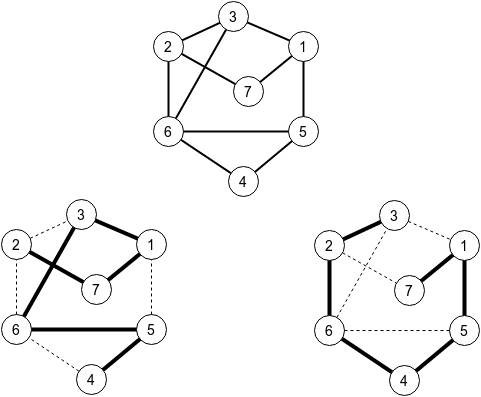
Solution:

#include <bits/stdc++.h>

using namespace std;

int main() {
int n, k;
int a, b, c, d;
scanf("%d %d", &n, &k);
scanf("%d %d %d %d", &a, &b, &c, &d);
if (n == 4 || k <= n) {
    printf("%d\n", -1);
    return 0;
  }

  vector <int> z;
for (int i = 1; i <= n; i++) {
    if (i != a && i != b && i != c && i != d) {
      z.push_back(i);
    }
  }

  int x = z.back();
  z.pop_back();

  printf("%d", a);
  for (int i = 0; i < (int) z.size(); i++) {
    printf(" %d", z[i]);
  }
  printf(" %d %d %d %d\n", c, x, d, b);

  printf("%d", c);
  for (int i = (int) z.size() - 1; i >= 0; i--) {
printf(" %d", z[i]);
}
printf(" %d %d %d %d\n", a, x, b, d);

return 0;
}