Table of Contents
1. Resolution
Resolution is a theorem proving technique that proceeds by building refutation proofs, i.e., proofs by contradictions. It was invented by a Mathematician John Alan Robinson in the year 1965.
Resolution is used, if there are various statements are given, and we need to prove a conclusion of those statements. Unification is a key concept in proofs by resolutions. Resolution is a single inference rule which can efficiently operate on the conjunctive normal form or clausal form.
Clause: Disjunction of literals (an atomic sentence) is called a clause. It is also known as a unit clause.
Conjunctive Normal Form: A sentence represented as a conjunction of clauses is said to be conjunctive normal form or CNF.
Note: To better understand this topic, firstly learns the FOL in AI.
2. The resolution inference rule:
The resolution rule for first-order logic is simply a lifted version of the propositional rule. Resolution can resolve two clauses if they contain complementary literals, which are assumed to be standardized apart so that they share no variables.

Where li and mj are complementary literals.
This rule is also called the binary resolution rule because it only resolves exactly two literals.
2.1. Example:
We can resolve two clauses which are given below:
[Animal (g(x) V Loves (f(x), x)] and [¬ Loves(a, b) V ¬Kills(a, b)]
Where two complimentary literals are: Loves (f(x), x) and ¬ Loves (a, b)
These literals can be unified with unifier θ= [a/f(x), and b/x] , and it will generate a resolvent clause:
[Animal (g(x) V ¬ Kills(f(x), x)].
3. Steps for Resolution:
- Conversion of facts into first-order logic.
- Convert FOL statements into CNF
- Negate the statement which needs to prove (proof by contradiction)
- Draw resolution graph (unification).
To better understand all the above steps, we will take an example in which we will apply resolution.
Example:
- John likes all kind of food.
- Apple and vegetable are food
- Anything anyone eats and not killed is food.
- Anil eats peanuts and still alive
- Harry eats everything that Anil eats.
Prove by resolution that: - John likes peanuts.
Step-1: Conversion of Facts into FOL
In the first step we will convert all the given statements into its first order logic.

Step-2: Conversion of FOL into CNF
In First order logic resolution, it is required to convert the FOL into CNF as CNF form makes easier for resolution proofs.
- Eliminate all implication (→) and rewrite
- ∀x ¬ food(x) V likes(John, x)
- food(Apple) Λ food(vegetables)
- ∀x ∀y ¬ [eats(x, y) Λ ¬ killed(x)] V food(y)
- eats (Anil, Peanuts) Λ alive(Anil)
- ∀x ¬ eats(Anil, x) V eats(Harry, x)
- ∀x¬ [¬ killed(x) ] V alive(x)
- ∀x ¬ alive(x) V ¬ killed(x)
- likes(John, Peanuts).
- Move negation (¬)inwards and rewrite
- ∀x ¬ food(x) V likes(John, x)
- food(Apple) Λ food(vegetables)
- ∀x ∀y ¬ eats(x, y) V killed(x) V food(y)
- eats (Anil, Peanuts) Λ alive(Anil)
- ∀x ¬ eats(Anil, x) V eats(Harry, x)
- ∀x ¬killed(x) ] V alive(x)
- ∀x ¬ alive(x) V ¬ killed(x)
- likes(John, Peanuts).
- Rename variables or standardize variables
- ∀x ¬ food(x) V likes(John, x)
- food(Apple) Λ food(vegetables)
- ∀y ∀z ¬ eats(y, z) V killed(y) V food(z)
- eats (Anil, Peanuts) Λ alive(Anil)
- ∀w¬ eats(Anil, w) V eats(Harry, w)
- ∀g ¬killed(g) ] V alive(g)
- ∀k ¬ alive(k) V ¬ killed(k)
- likes(John, Peanuts).
- Eliminate existential instantiation quantifier by elimination.
In this step, we will eliminate existential quantifier ∃, and this process is known as Skolemization. But in this example problem since there is no existential quantifier so all the statements will remain same in this step. - Drop Universal quantifiers.
In this step we will drop all universal quantifier since all the statements are not implicitly quantified so we don’t need it.- ¬ food(x) V likes(John, x)
- food(Apple)
- food(vegetables)
- ¬ eats(y, z) V killed(y) V food(z)
- eats (Anil, Peanuts)
- alive(Anil)
- ¬ eats(Anil, w) V eats(Harry, w)
- killed(g) V alive(g)
- ¬ alive(k) V ¬ killed(k)
- likes(John, Peanuts).
Note: Statements “food(Apple) Λ food(vegetables)” and “eats (Anil, Peanuts) Λ alive(Anil)” can be written in two separate statements.
- Distribute conjunction ∧ over disjunction ¬.
This step will not make any change in this problem.
Step-3: Negate the statement to be proved
In this statement, we will apply negation to the conclusion statements, which will be written as ¬likes(John, Peanuts)
Step-4: Draw Resolution graph:
Now in this step, we will solve the problem by resolution tree using substitution. For the above problem, it will be given as follows:
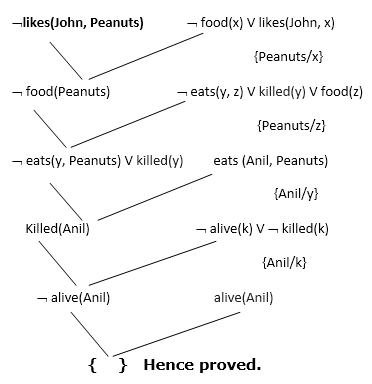
Hence the negation of the conclusion has been proved as a complete contradiction with the given set of statements.
4. Explanation of Resolution graph:
- In the first step of resolution graph, ¬likes(John, Peanuts) , and likes(John, x) get resolved(canceled) by substitution of {Peanuts/x}, and we are left with ¬ food(Peanuts)
- In the second step of the resolution graph, ¬ food(Peanuts) , and food(z) get resolved (canceled) by substitution of { Peanuts/z}, and we are left with ¬ eats(y, Peanuts) V killed(y) .
- In the third step of the resolution graph, ¬ eats(y, Peanuts) and eats (Anil, Peanuts) get resolved by substitution {Anil/y}, and we are left with Killed(Anil) .
- In the fourth step of the resolution graph, Killed(Anil) and ¬ killed(k) get resolve by substitution {Anil/k}, and we are left with ¬ alive(Anil) .
- In the last step of the resolution graph ¬ alive(Anil) and alive(Anil) get resolved.

