PolandBall and Polygon

PolandBall has such a convex polygon with n veritces that no three of its diagonals intersect at the same point. PolandBall decided to improve it and draw some red segments.

He chose a number k such that gcd(n, k) = 1. Vertices of the polygon are numbered from 1 to n in a clockwise way. PolandBall repeats the following process n times, starting from the vertex 1:

Assume you’ve ended last operation in vertex x (consider x = 1 if it is the first operation). Draw a new segment from vertex x to k-th next vertex in clockwise direction. This is a vertex x + k or x + k - n depending on which of these is a valid index of polygon’s vertex.

Your task is to calculate number of polygon’s sections after each drawing. A section is a clear area inside the polygon bounded with drawn diagonals or the polygon’s sides.

Input

There are only two numbers in the input: n and k (5 ≤ n ≤ 10⁶, 2 ≤ k ≤ n - 2, gcd(n, k) = 1).

Output

You should print n values separated by spaces. The i-th value should represent number of polygon’s sections after drawing first i lines.

Examples

input

5 2

output

2 3 5 8 11 

input

10 3

output

2 3 4 6 9 12 16 21 26 31 

Note

The greatest common divisor (gcd) of two integers a and b is the largest positive integer that divides both a and b without a remainder.

For the first sample testcase, you should output “2 3 5 8 11”. Pictures below correspond to situations after drawing lines.

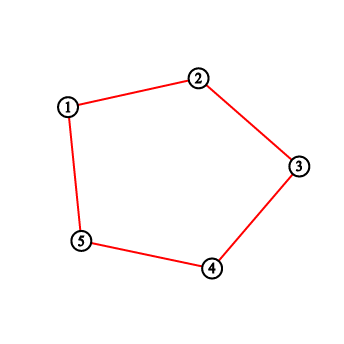
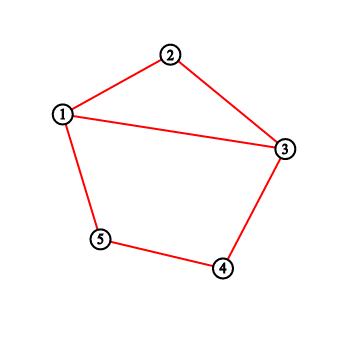
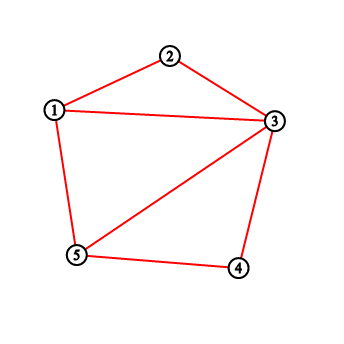
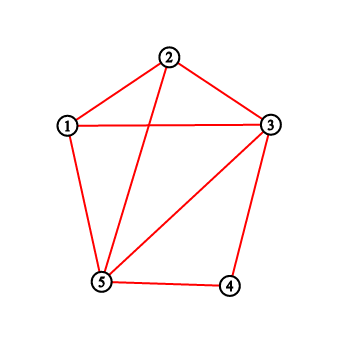
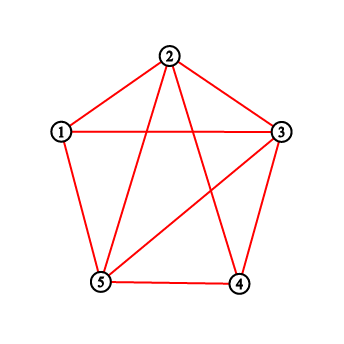
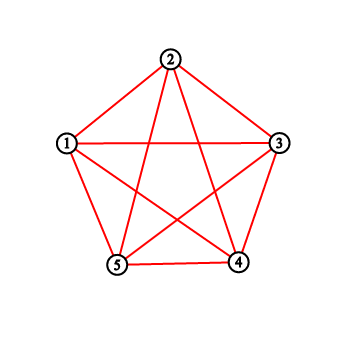
Solution:

#include <bits/stdc++.h>

using namespace std;

const int N = 3234567;

int fenw[N];
int n;

void modify(int x, int v) {
while (x <= n) {
    fenw[x] += v;
    x = (x | (x - 1)) + 1;
  }
}

int find_sum(int x) {
  int v = 0;
  while (x > 0) {
v += fenw[x];
x &= x - 1;
}
return v;
}

int main() {
int k;
scanf("%d %d", &n, &k);
if (2 * k > n) {
k = n - k;
}
for (int i = 1; i <= n; i++) {
    fenw[i] = 0;
  }
  int x = 1;
  long long ans = 1;
  for (int it = 1; it <= n; it++) {
    ans++;
    int from = x - k + 1;
    int to = x + k - 1;
    if (from < 1) {
      ans += find_sum(to) + find_sum(n) - find_sum(from + n - 1);
    } else {
      if (to > n) {
ans += find_sum(n) - find_sum(from - 1) + find_sum(to - n);
} else {
ans += find_sum(to) - find_sum(from - 1);
}
}
modify(x, 1);
x += k;
if (x > n) {
x -= n;
}
if (it > 1) putchar(' ');
printf("%I64d", ans);
}
printf("\n");
return 0;
}