Koala and Lights

It is a holiday season, and Koala is decorating his house with cool lights! He owns $n$ lights, all of which flash periodically.

After taking a quick glance at them, Koala realizes that each of his lights can be described with two parameters $a_i$ and $b_i$. Light with parameters $a_i$ and $b_i$ will toggle (on to off, or off to on) every $a_i$ seconds starting from the $b_i$-th second. In other words, it will toggle at the moments $b_i$, $b_i + a_i$, $b_i + 2 \cdot a_i$ and so on.

You know for each light whether it’s initially on or off and its corresponding parameters $a_i$ and $b_i$. Koala is wondering what is the maximum number of lights that will ever be on at the same time. So you need to find that out.

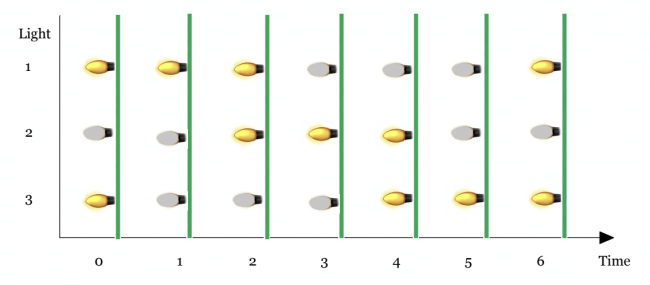
Here is a graphic for the first example.

Input

The first line contains a single integer $n$ ($1 \le n \le 100$), the number of lights.

The next line contains a string $s$ of $n$ characters. The $i$-th character is “1”, if the $i$-th lamp is initially on. Otherwise, $i$-th character is “0”.

The $i$-th of the following $n$ lines contains two integers $a_i$ and $b_i$ ($1 \le a_i, b_i \le 5$)  — the parameters of the $i$-th light.

Output

Print a single integer — the maximum number of lights that will ever be on at the same time.

Examples

input

3
101
3 3
3 2
3 1

Output

2

input

4
1111
3 4
5 2
3 1
3 2

output

4

input

6
011100
5 3
5 5
2 4
3 5
4 2
1 5

output

6

Note

For first example, the lamps’ states are shown in the picture above. The largest number of simultaneously on lamps is $2$ (e.g. at the moment $2$).

In the second example, all lights are initially on. So the answer is $4$.

Solution:

#include <bits/stdc++.h>

using namespace std;

int main() {
ios::sync_with_stdio(false);
cin.tie(0);
const int MAX = 100000;
vector<int> cnt(MAX);
int n;
cin >> n;
string s;
cin >> s;
for (int i = 0; i < n; i++) {
    int a, b;
    cin >> a >> b;
int c = (int) (s[i] - '0');
for (int j = 0; j < MAX; j++) {
      cnt[j] += c;
      if (j == b) {
        c ^= 1;
        b += a;
      }
    }
  }
  cout << *max_element(cnt.begin(), cnt.end()) << '\n';
  return 0;
}