Prim’s Algorithm

In this tutorial, you will learn how Prim’s Algorithm works. Also, you will find working examples of Prim’s Algorithm in C, C++, Java and Python.

Prim’s algorithm is a minimum spanning tree algorithm that takes a graph as input and finds the subset of the edges of that graph which

• form a tree that includes every vertex
• has the minimum sum of weights among all the trees that can be formed from the graph

1. How Prim’s algorithm works

It falls under a class of algorithms called greedy algorithms that find the local optimum in the hopes of finding a global optimum.

We start from one vertex and keep adding edges with the lowest weight until we reach our goal.

The steps for implementing Prim’s algorithm are as follows:

1. Initialize the minimum spanning tree with a vertex chosen at random.
2. Find all the edges that connect the tree to new vertices, find the minimum and add it to the tree
3. Keep repeating step 2 until we get a minimum spanning tree

2. Example of Prim’s algorithm

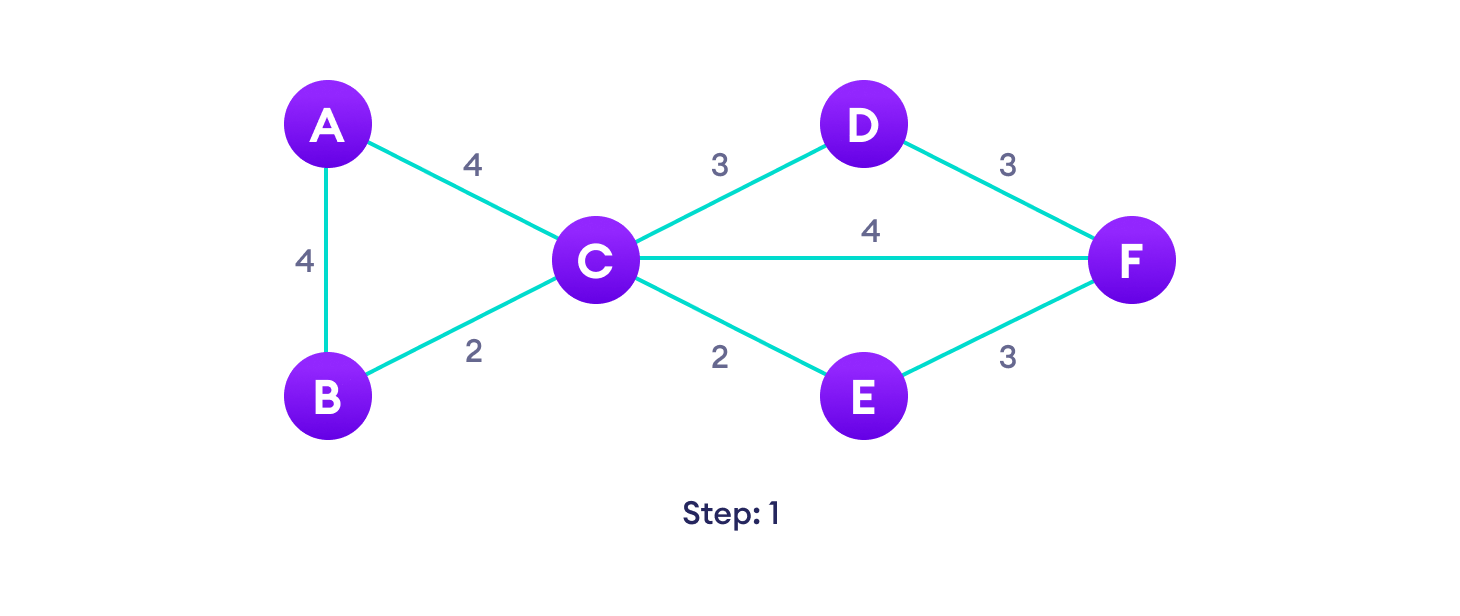
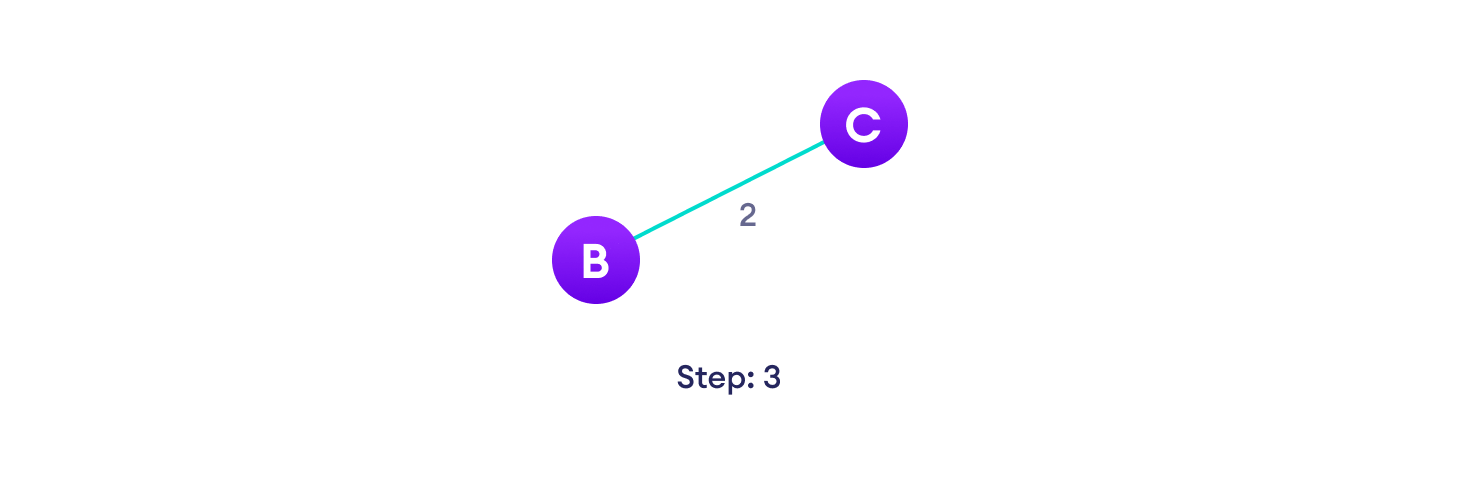
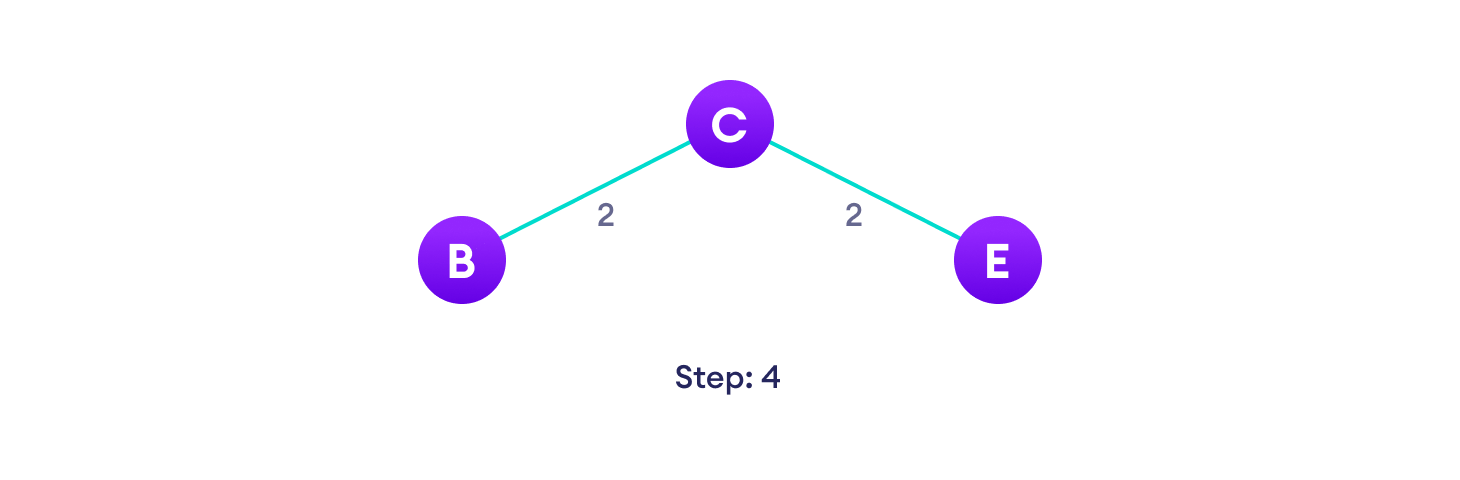
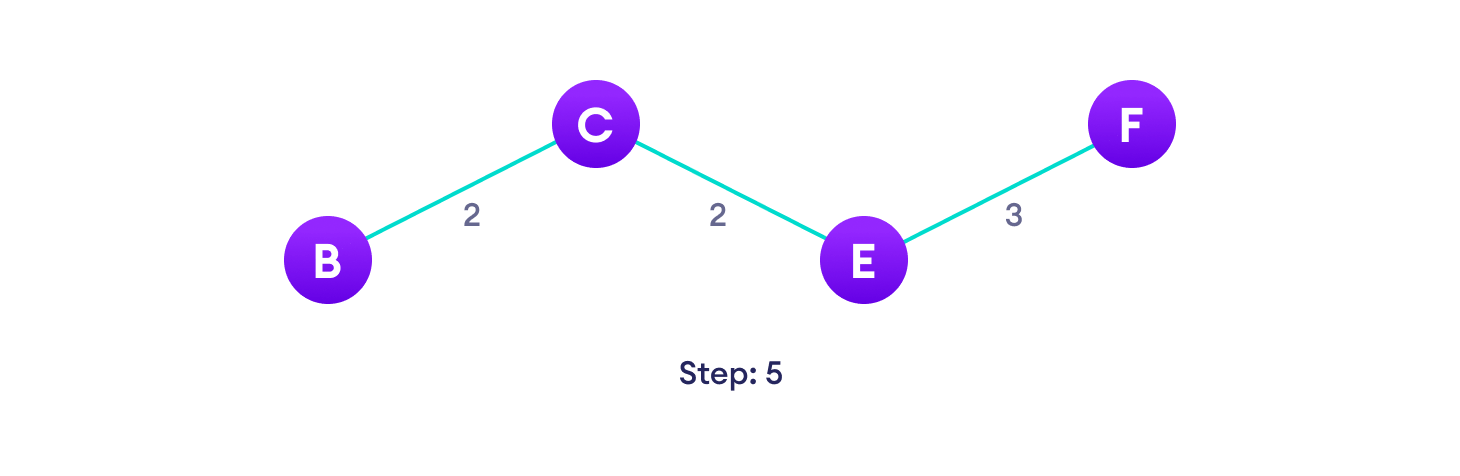
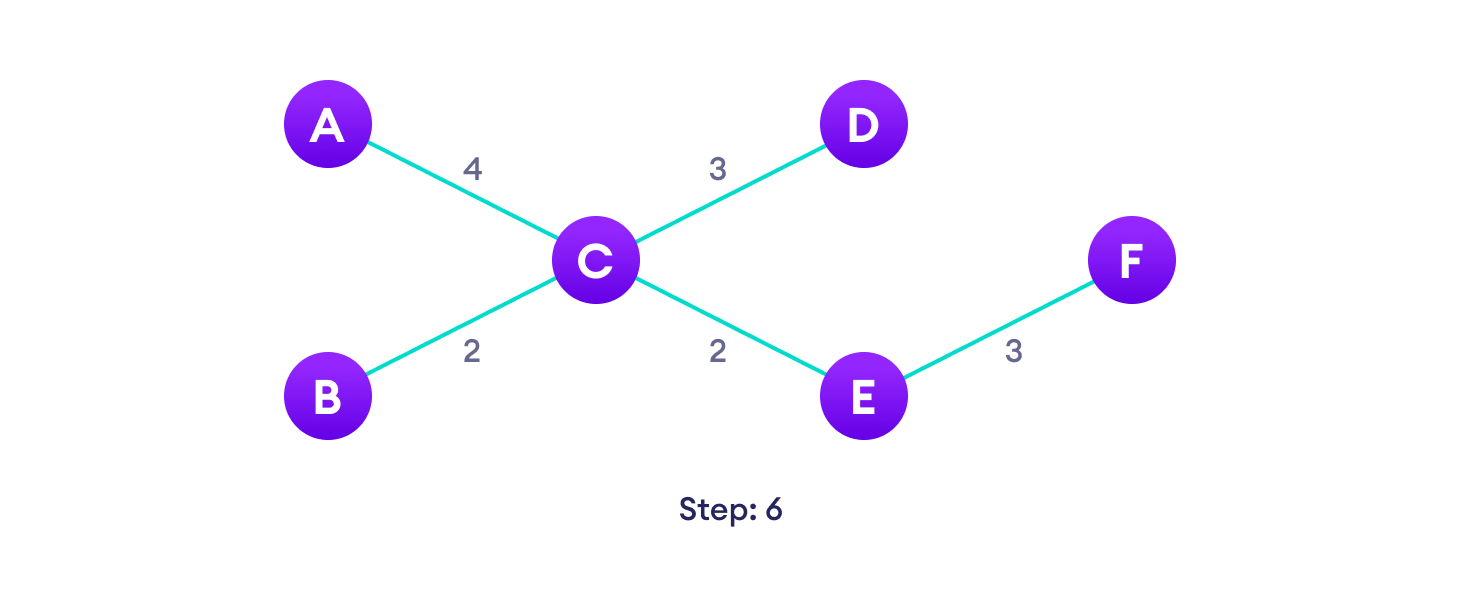
3. Prim’s Algorithm pseudocode

The pseudocode for prim’s algorithm shows how we create two sets of vertices U and V-U. U contains the list of vertices that have been visited and V-U the list of vertices that haven’t. One by one, we move vertices from set V-U to set U by connecting the least weight edge.

T = ∅;
U = { 1 };
while (U ≠ V)
    let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U;
    T = T ∪ {(u, v)}
    U = U ∪ {v}

4. Python, Java and C/C++ Examples

Although adjacency matrix representation of graphs is used, this algorithm can also be implemented using Adjacency List to improve its efficiency.

Source code by Python Language:

# Prim's Algorithm in Python


INF = 9999999
# number of vertices in graph
V = 5
# create a 2d array of size 5x5
# for adjacency matrix to represent graph
G = [[0, 9, 75, 0, 0],
     [9, 0, 95, 19, 42],
     [75, 95, 0, 51, 66],
     [0, 19, 51, 0, 31],
     [0, 42, 66, 31, 0]]
# create a array to track selected vertex
# selected will become true otherwise false
selected = [0, 0, 0, 0, 0]
# set number of edge to 0
no_edge = 0
# the number of egde in minimum spanning tree will be
# always less than(V - 1), where V is number of vertices in
# graph
# choose 0th vertex and make it true
selected[0] = True
# print for edge and weight
print("Edge : Weight\n")
while (no_edge < V - 1):
    # For every vertex in the set S, find the all adjacent vertices
    #, calculate the distance from the vertex selected at step 1.
    # if the vertex is already in the set S, discard it otherwise
    # choose another vertex nearest to selected vertex  at step 1.
    minimum = INF
    x = 0
    y = 0
    for i in range(V):
        if selected[i]:
            for j in range(V):
                if ((not selected[j]) and G[i][j]):  
                    # not in selected and there is an edge
                    if minimum > G[i][j]:
                        minimum = G[i][j]
                        x = i
                        y = j
    print(str(x) + "-" + str(y) + ":" + str(G[x][y]))
    selected[y] = True
    no_edge += 1

Source code by Java Language:

// Prim's Algorithm in Java

import java.util.Arrays;

class PGraph {

  public void Prim(int G[][], int V) {

    int INF = 9999999;

    int no_edge; // number of edge

    // create a array to track selected vertex
    // selected will become true otherwise false
    boolean[] selected = new boolean[V];

    // set selected false initially
    Arrays.fill(selected, false);

    // set number of edge to 0
    no_edge = 0;

    // the number of egde in minimum spanning tree will be
    // always less than (V -1), where V is number of vertices in
    // graph

    // choose 0th vertex and make it true
    selected[0] = true;

    // print for edge and weight
    System.out.println("Edge : Weight");

    while (no_edge < V - 1) {
      // For every vertex in the set S, find the all adjacent vertices
      // , calculate the distance from the vertex selected at step 1.
      // if the vertex is already in the set S, discard it otherwise
      // choose another vertex nearest to selected vertex at step 1.

      int min = INF;
      int x = 0; // row number
      int y = 0; // col number

      for (int i = 0; i < V; i++) {
        if (selected[i] == true) {
          for (int j = 0; j < V; j++) {
            // not in selected and there is an edge
            if (!selected[j] && G[i][j] != 0) {
              if (min > G[i][j]) {
                min = G[i][j];
                x = i;
                y = j;
              }
            }
          }
        }
      }
      System.out.println(x + " - " + y + " :  " + G[x][y]);
      selected[y] = true;
      no_edge++;
    }
  }

  public static void main(String[] args) {
    PGraph g = new PGraph();

    // number of vertices in grapj
    int V = 5;

    // create a 2d array of size 5x5
    // for adjacency matrix to represent graph
    int[][] G = { { 0, 9, 75, 0, 0 }, { 9, 0, 95, 19, 42 }, { 75, 95, 0, 51, 66 }, { 0, 19, 51, 0, 31 },
        { 0, 42, 66, 31, 0 } };

    g.Prim(G, V);
  }
}

Source code by C Language:

// Prim's Algorithm in C

#include<stdio.h>
#include<stdbool.h> 

#define INF 9999999

// number of vertices in graph
#define V 5

// create a 2d array of size 5x5
//for adjacency matrix to represent graph
int G[V][V] = {
  {0, 9, 75, 0, 0},
  {9, 0, 95, 19, 42},
  {75, 95, 0, 51, 66},
  {0, 19, 51, 0, 31},
  {0, 42, 66, 31, 0}};

int main() {
  int no_edge;  // number of edge

  // create a array to track selected vertex
  // selected will become true otherwise false
  int selected[V];

  // set selected false initially
  memset(selected, false, sizeof(selected));
  
  // set number of edge to 0
  no_edge = 0;

  // the number of egde in minimum spanning tree will be
  // always less than (V -1), where V is number of vertices in
  //graph

  // choose 0th vertex and make it true
  selected[0] = true;

  int x;  //  row number
  int y;  //  col number

  // print for edge and weight
  printf("Edge : Weight\n");

  while (no_edge < V - 1) {
    //For every vertex in the set S, find the all adjacent vertices
    // , calculate the distance from the vertex selected at step 1.
    // if the vertex is already in the set S, discard it otherwise
    //choose another vertex nearest to selected vertex  at step 1.

    int min = INF;
    x = 0;
    y = 0;

    for (int i = 0; i < V; i++) {
      if (selected[i]) {
        for (int j = 0; j < V; j++) {
          if (!selected[j] && G[i][j]) {  // not in selected and there is an edge
            if (min > G[i][j]) {
              min = G[i][j];
              x = i;
              y = j;
            }
          }
        }
      }
    }
    printf("%d - %d : %d\n", x, y, G[x][y]);
    selected[y] = true;
    no_edge++;
  }

  return 0;
}

Source code by C++ Language:

// Prim's Algorithm in C++

#include <cstring>
#include <iostream>
using namespace std;

#define INF 9999999

// number of vertices in grapj
#define V 5

// create a 2d array of size 5x5
//for adjacency matrix to represent graph

int G[V][V] = {
  {0, 9, 75, 0, 0},
  {9, 0, 95, 19, 42},
  {75, 95, 0, 51, 66},
  {0, 19, 51, 0, 31},
  {0, 42, 66, 31, 0}};

int main() {
  int no_edge;  // number of edge

  // create a array to track selected vertex
  // selected will become true otherwise false
  int selected[V];

  // set selected false initially
  memset(selected, false, sizeof(selected));

  // set number of edge to 0
  no_edge = 0;

  // the number of egde in minimum spanning tree will be
  // always less than (V -1), where V is number of vertices in
  //graph

  // choose 0th vertex and make it true
  selected[0] = true;

  int x;  //  row number
  int y;  //  col number

  // print for edge and weight
  cout << "Edge"
     << " : "
     << "Weight";
  cout << endl;
  while (no_edge < V - 1) {
    //For every vertex in the set S, find the all adjacent vertices
    // , calculate the distance from the vertex selected at step 1.
    // if the vertex is already in the set S, discard it otherwise
    //choose another vertex nearest to selected vertex  at step 1.

    int min = INF;
    x = 0;
    y = 0;

    for (int i = 0; i < V; i++) {
      if (selected[i]) {
        for (int j = 0; j < V; j++) {
          if (!selected[j] && G[i][j]) {  // not in selected and there is an edge
            if (min > G[i][j]) {
              min = G[i][j];
              x = i;
              y = j;
            }
          }
        }
      }
    }
    cout << x << " - " << y << " :  " << G[x][y];
    cout << endl;
    selected[y] = true;
    no_edge++;
  }

  return 0;
}

5. Prim’s vs Kruskal’s Algorithm

Kruskal’s algorithm is another popular minimum spanning tree algorithm that uses a different logic to find the MST of a graph. Instead of starting from a vertex, Kruskal’s algorithm sorts all the edges from low weight to high and keeps adding the lowest edges, ignoring those edges that create a cycle.

6. Prim’s Algorithm Complexity

The time complexity of Prim’s algorithm is O(E log V).

7. Prim’s Algorithm Application

• Laying cables of electrical wiring
• In network designed
• To make protocols in network cycles